L2 Normalization
论文:ParseNet: Looking Wider to See Better,link
L2 Normalization layers
这篇语义分割的文章提出使用 \(L_2\) Normalization layers。问题提出的结构如下图所示:
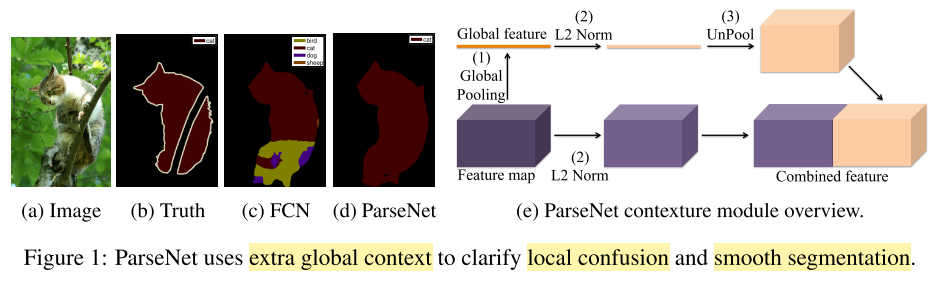
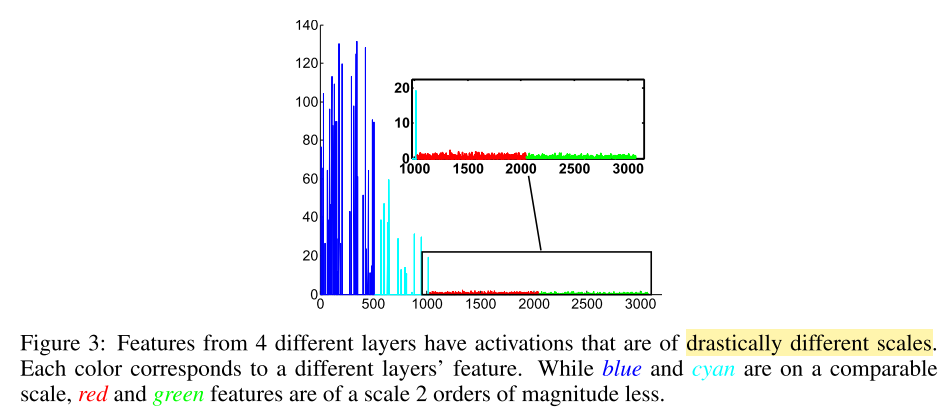
如图3所示,当我们需要组合两个或者更多的特征向量时,它们通常有不同的尺度和范数。简单的级联特征导致较差的性能,因为比较大的特征会主导较小的特征。虽然在训练期间,权重可能会相应调整,但需要非常仔细地调整参数,并且依赖于数据集,因此违背了稳健原则。我们发现,通过首先规范每个单独的特征,并学习以不同尺度进行放缩,这使得训练更加稳定,并且可以提高性能。
\(L_2\) 范数层不仅在特征组合的时候使用。如上所述,在某些情况下,后期融合也同样有效,但仅在L2归一化的帮助下。例如,如果我们想使用底层的特征去学习分类器,如图3所示,一些特征可能有很大的范数。在没有只是的权重初始化和参数调整的情况下,这非常困难。关于这个策略的一个工作就是使用一个附加的卷积层,并且使用多级微调,例如底层使用更小的学习率。这违反了简单和鲁棒的原则。在这篇论文的工作中,对分类之前的特征的每个通道,作者使用了\(L_2\)-norm并且学习了缩放参数,这导致了更加稳定的训练。
对于一个d维的输入 \(\mathbf{x}=(x_1, ..., x_d)\),我们使用 \(L_2\)-norm 规范它,即 \(\hat{x}=\frac{x}{\lVert x \rVert_2}\),其中 \(\lVert x \rVert_2=(\sum_{i=1}^{d} {\lvert x_i \rvert}^2)^{1/2}\) 是 \(\mathbf{x}\) 的 \(L_2\) 范数。
请注意,如果我们不相应地缩放它,只简单地规范化层的每个输入会改变层的尺度,将会减慢学习速度。例如,我们尝试规范化功能 s.t. \(L_2\)-norm 是1,但我们很难训练网络,因为特征变得非常小。 但是,如果我们将其规范化为,例如 10 或 20,网络开始较好的学习。在 batch normalization 和 PReLU 的推动下,我们为每个通道引入缩放参数 \(\gamma_i\),它缩放了归一化的值 \(y_i=\gamma_i \hat{x}_i\)。
额外参数的数量等于通道的总数,并且可以忽略不计,并且可以通过反向传播来学习。 实际上,通过设置 \(\gamma_i={\lVert x_i \rVert}^2\),我们可以恢复 \(L_2\) 归一化的特征。这很容易实现,因为规范化和缩放参数学习仅依赖于每个输入特征向量,并且不需要像批量规范化那样聚合来自其他样本的信息。在训练期间,我们使用反向传播和链规则来计算关于缩放银子 \(\gamma\) 和输入数据 \(\mathbf{x}\) 的导数。
Pytorch Code
1 | import torch.nn.functional as F |
1 | import torch |